how to find end behavior
Learning Outcomes
- Identify polynomial functions.
- Identify the degree and leading coefficient of polynomial functions.
- Describe the end behavior of a polynomial function.
Identifying Polynomial Functions
An oil pipeline bursts in the Gulf of Mexico causing an oil slick in a roughly circular shape. The slick is currently 24 miles in radius, but that radius is increasing by 8 miles each week. We want to write a formula for the area covered by the oil slick by combining two functions. The radius r of the spill depends on the number of weeks w that have passed. This relationship is linear.
[latex]r\left(w\right)=24+8w[/latex]
We can combine this with the formula for the area A of a circle.
[latex]A\left(r\right)=\pi {r}^{2}[/latex]
Composing these functions gives a formula for the area in terms of weeks.
[latex]\begin{array}{l}A\left(w\right)=A\left(r\left(w\right)\right)\\ A\left(w\right)=A\left(24+8w\right)\\ A\left(w\right)=\pi {\left(24+8w\right)}^{2}\end{array}[/latex]
Multiplying gives the formula below.
[latex]A\left(w\right)=576\pi +384\pi w+64\pi {w}^{2}[/latex]
This formula is an example of a polynomial function. A polynomial function consists of either zero or the sum of a finite number of non-zero terms, each of which is a product of a number, called the coefficient of the term, and a variable raised to a non-negative integer power.
A General Note: Polynomial Functions
Let n be a non-negative integer. A polynomial function is a function that can be written in the form
[latex]f\left(x\right)={a}_{n}{x}^{n}+\dots+{a}_{2}{x}^{2}+{a}_{1}x+{a}_{0}[/latex]
This is called the general form of a polynomial function. Each [latex]{a}_{i}[/latex] is a coefficient and can be any real number. Each product [latex]{a}_{i}{x}^{i}[/latex] is a term of a polynomial function.
Example: Identifying Polynomial Functions
Which of the following are polynomial functions?
[latex]\begin{array}{c}f\left(x\right)=2{x}^{3}\cdot 3x+4\hfill \\ g\left(x\right)=-x\left({x}^{2}-4\right)\hfill \\ h\left(x\right)=5\sqrt{x}+2\hfill \end{array}[/latex]
Try It
Defining the Degree and Leading Coefficient of a Polynomial Function
Because of the form of a polynomial function, we can see an infinite variety in the number of terms and the power of the variable. Although the order of the terms in the polynomial function is not important for performing operations, we typically arrange the terms in descending order based on the power on the variable. This is called writing a polynomial in general or standard form. The degree of the polynomial is the highest power of the variable that occurs in the polynomial; it is the power of the first variable if the function is in general form. The leading term is the term containing the variable with the highest power, also called the term with the highest degree. The leading coefficient is the coefficient of the leading term.
A General Note: Terminology of Polynomial Functions

We often rearrange polynomials so that the powers on the variable are descending.
When a polynomial is written in this way, we say that it is in general form.
How To: Given a polynomial function, identify the degree and leading coefficient
- Find the highest power of xto determine the degree of the function.
- Identify the term containing the highest power of xto find the leading term.
- The leading coefficient is the coefficient of the leading term.
Example: Identifying the Degree and Leading Coefficient of a Polynomial Function
Identify the degree, leading term, and leading coefficient of the following polynomial functions.
[latex]\begin{array}{l} f\left(x\right)=3+2{x}^{2}-4{x}^{3} \\g\left(t\right)=5{t}^{5}-2{t}^{3}+7t\\h\left(p\right)=6p-{p}^{3}-2\end{array}[/latex]
Try It
Identify the degree, leading term, and leading coefficient of the polynomial [latex]f\left(x\right)=4{x}^{2}-{x}^{6}+2x - 6[/latex].
Show Solution
The degree is 6. The leading term is [latex]-{x}^{6}[/latex]. The leading coefficient is [latex]–1[/latex].
In the following video, we show more examples of how to determine the degree, leading term, and leading coefficient of a polynomial.
Identifying End Behavior of Polynomial Functions
Knowing the leading coefficient and degree of a polynomial function is useful when predicting its end behavior. To determine its end behavior, look at the leading term of the polynomial function. Because the power of the leading term is the highest, that term will grow significantly faster than the other terms as x gets very large or very small, so its behavior will dominate the graph. For any polynomial, the end behavior of the polynomial will match the end behavior of the term of highest degree.
| Polynomial Function | Leading Term | Graph of Polynomial Function |
|---|---|---|
| [latex]f\left(x\right)=5{x}^{4}+2{x}^{3}-x - 4[/latex] | [latex]5{x}^{4}[/latex] |  |
| [latex]f\left(x\right)=-2{x}^{6}-{x}^{5}+3{x}^{4}+{x}^{3}[/latex] | [latex]-2{x}^{6}[/latex] |  |
| [latex]f\left(x\right)=3{x}^{5}-4{x}^{4}+2{x}^{2}+1[/latex] | [latex]3{x}^{5}[/latex] |  |
| [latex]f\left(x\right)=-6{x}^{3}+7{x}^{2}+3x+1[/latex] | [latex]-6{x}^{3}[/latex] |  |
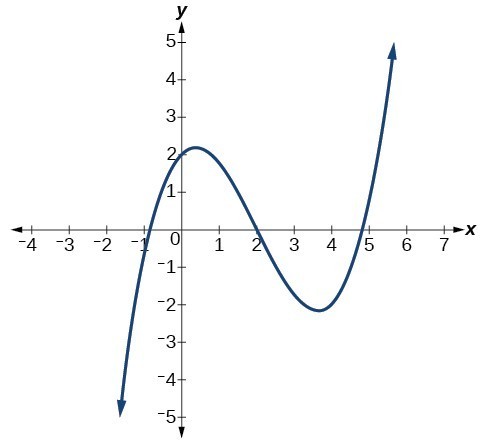
Example: Identifying End Behavior and Degree of a Polynomial Function
Describe the end behavior and determine a possible degree of the polynomial function in the graph below.
In the following video, we show more examples that summarize the end behavior of polynomial functions and which components of the function contribute to it.
Try It
Describe the end behavior of the polynomial function in the graph below.

Show Solution
As [latex]x\to \infty , f\left(x\right)\to -\infty[/latex] and as [latex]x\to -\infty , f\left(x\right)\to -\infty [/latex]. It has the shape of an even degree power function with a negative coefficient.
Example: Identifying End Behavior and Degree of a Polynomial Function
Given the function [latex]f\left(x\right)=-3{x}^{2}\left(x - 1\right)\left(x+4\right)[/latex], express the function as a polynomial in general form and determine the leading term, degree, and end behavior of the function.
Try It
Given the function [latex]f\left(x\right)=0.2\left(x - 2\right)\left(x+1\right)\left(x - 5\right)[/latex], express the function as a polynomial in general form and determine the leading term, degree, and end behavior of the function.
Show Solution
The leading term is [latex]0.2{x}^{3}[/latex], so it is a degree 3 polynomial. As x approaches positive infinity, [latex]f\left(x\right)[/latex] increases without bound; as x approaches negative infinity, [latex]f\left(x\right)[/latex] decreases without bound.
Contribute!
Did you have an idea for improving this content? We'd love your input.
Improve this pageLearn More
how to find end behavior
Source: https://courses.lumenlearning.com/waymakercollegealgebra/chapter/end-behavior-of-polynomial-functions/#:~:text=To%20determine%20its%20end%20behavior,behavior%20will%20dominate%20the%20graph.
Posted by: flowersdowanceares.blogspot.com

0 Response to "how to find end behavior"
Post a Comment